Profile

We present a new method to compute continuous and bijective maps (surface homeomorphisms) between two or more genus-0 triangle meshes. In contrast to previous approaches, we decouple the resolution at which a map is represented from the resolution of the input meshes. We discretize maps via common triangulations that approximate the input meshes while remaining in bijective correspondence to them. Both the geometry and the connectivity of these triangulations are optimized with respect to a single objective function that simultaneously controls mapping distortion, triangulation quality, and approximation error. A discrete-continuous optimization algorithm performs both energy-based remeshing as well as global second-order optimization of vertex positions, parametrized via the sphere. With this, we combine the disciplines of compatible remeshing and surface map optimization in a unified formulation and make a contribution in both fields. While existing compatible remeshing algorithms often operate on a fixed pre-computed surface map, we can now globally update this correspondence during remeshing. On the other hand, bijective surface-to-surface map optimization previously required computing costly overlay meshes that are inherently tied to the input mesh resolution. We achieve significant complexity reduction by instead assessing distortion between the approximating triangulations. This new map representation is inherently more robust than previous overlay-based approaches, is less intricate to implement, and naturally supports mapping between more than two surfaces. Moreover, it enables adaptive multi-resolution schemes that, e.g., first align corresponding surface regions at coarse resolutions before refining the map where needed. We demonstrate significant speedups and increased flexibility over state-of-the art mapping algorithms at similar map quality, and also provide a reference implementation of the method.

• Günter Enderle Best Paper Award at Eurographics 2023
• Graphics Replicability Stamp

Non-linear optimization is essential to many areas of geometry processing research. However, when experimenting with different problem formulations or when prototyping new algorithms, a major practical obstacle is the need to figure out derivatives of objective functions, especially when second-order derivatives are required. Deriving and manually implementing gradients and Hessians is both time-consuming and error-prone. Automatic differentiation techniques address this problem, but can introduce a diverse set of obstacles themselves, e.g. limiting the set of supported language features, imposing restrictions on a program's control flow, incurring a significant run time overhead, or making it hard to exploit sparsity patterns common in geometry processing. We show that for many geometric problems, in particular on meshes, the simplest form of forward-mode automatic differentiation is not only the most flexible, but also actually the most efficient choice. We introduce TinyAD: a lightweight C++ library that automatically computes gradients and Hessians, in particular of sparse problems, by differentiating small (tiny) sub-problems. Its simplicity enables easy integration; no restrictions on, e.g., looping and branching are imposed. TinyAD provides the basic ingredients to quickly implement first and second order Newton-style solvers, allowing for flexible adjustment of both problem formulations and solver details. By showcasing compact implementations of methods from parametrization, deformation, and direction field design, we demonstrate how TinyAD lowers the barrier to exploring non-linear optimization techniques. This enables not only fast prototyping of new research ideas, but also improves replicability of existing algorithms in geometry processing. TinyAD is available to the community as an open source library.

• Best Paper Award (1st place) at SGP 2022
• Graphics Replicability Stamp

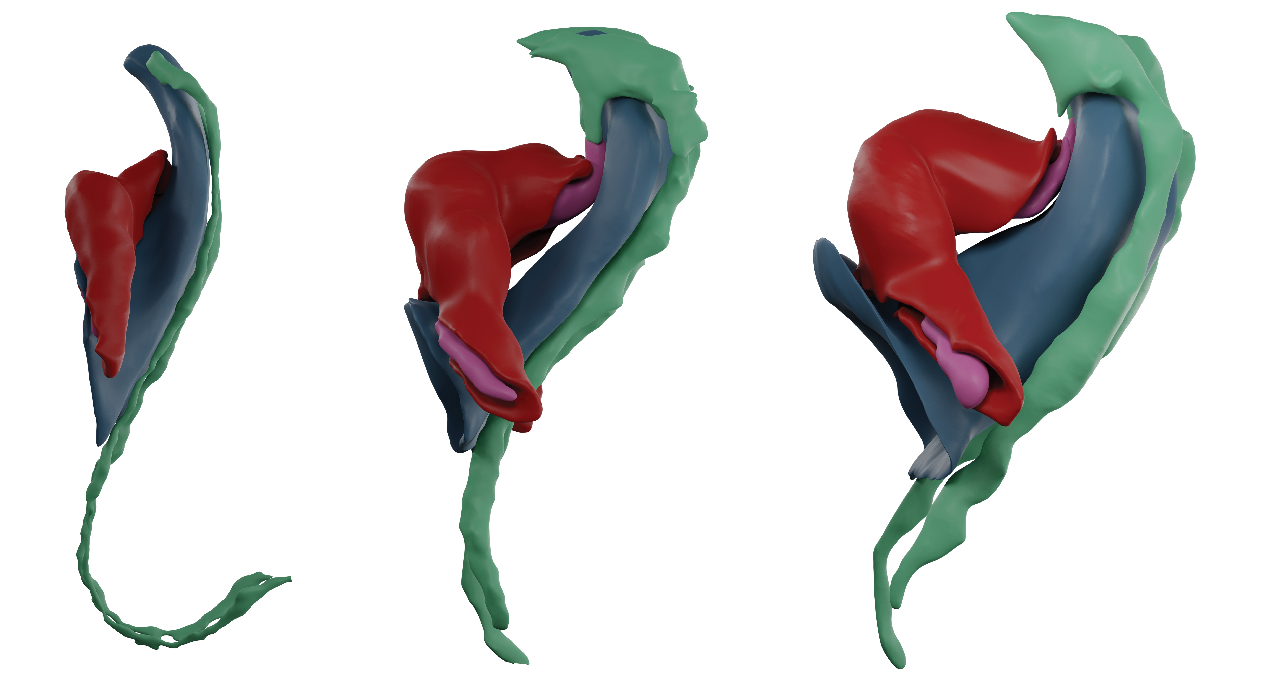
Understanding organ morphogenesis requires a precise geometrical description of the tissues involved in the process. The high morphological variability in mammalian embryos hinders the quantitative analysis of organogenesis. In particular, the study of early heart development in mammals remains a challenging problem due to imaging limitations and complexity. Here, we provide a complete morphological description of mammalian heart tube formation based on detailed imaging of a temporally dense collection of mouse embryonic hearts. We develop strategies for morphometric staging and quantification of local morphological variations between specimens. We identify hot spots of regionalized variability and identify Nodal-controlled left–right asymmetry of the inflow tracts as the earliest signs of organ left–right asymmetry in the mammalian embryo. Finally, we generate a three-dimensional+t digital model that allows co-representation of data from different sources and provides a framework for the computer modeling of heart tube formation.

A homeomorphism between two surfaces not only defines a (continuous and bijective) geometric correspondence of points but also (by implication) an identification of topological features, i.e. handles and tunnels, and how the map twists around them. However, in practice, surface maps are often encoded via sparse correspondences or fuzzy representations that merely approximate a homeomorphism and are therefore inherently ambiguous about map topology. In this work, we show a way to infer topological information from an imperfect input map between two shapes. In particular, we compute a homology map, a linear map that transports homology classes of cycles from one surface to the other, subject to a global consistency constraint. Our inference robustly handles imperfect (e.g., partial, sparse, fuzzy, noisy, outlier-ridden, non-injective) input maps and is guaranteed to produce homology maps that are compatible with true homeomorphisms between the input shapes. Homology maps inferred by our method can be directly used to transfer homological information between shapes, or serve as foundation for the construction of a proper homeomorphism guided by the input map, e.g., via compatible surface decomposition.

• Best Paper Award at SGP 2021
• Graphics Replicability Stamp

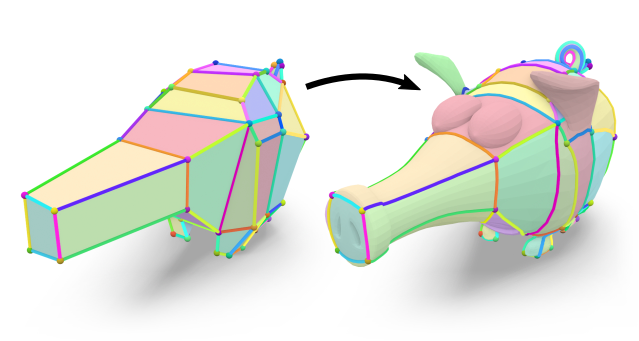
We consider the problem of injectively embedding a given graph connectivity (a layout) into a target surface. Starting from prescribed positions of layout vertices, the task is to embed all layout edges as intersection-free paths on the surface. Besides merely geometric choices (the shape of paths) this problem is especially challenging due to its topological degrees of freedom (how to route paths around layout vertices). The problem is typically addressed through a sequence of shortest path insertions, ordered by a greedy heuristic. Such insertion sequences are not guaranteed to be optimal: Early path insertions can potentially force later paths into unexpected homotopy classes. We show how common greedy methods can easily produce embeddings of dramatically bad quality, rendering such methods unsuitable for automatic processing pipelines. Instead, we strive to find the optimal order of insertions, i.e. the one that minimizes the total path length of the embedding. We demonstrate that, despite the vast combinatorial solution space, this problem can be effectively solved on simply-connected domains via a custom-tailored branch-and-bound strategy. This enables directly using the resulting embeddings in downstream applications which cannot recover from initializations in a wrong homotopy class. We demonstrate the robustness of our method on a shape dataset by embedding a common template layout per category, and show applications in quad meshing and inter-surface mapping.

• Honorable mention for Günter Enderle Best Paper Award
• Graphics Replicability Stamp

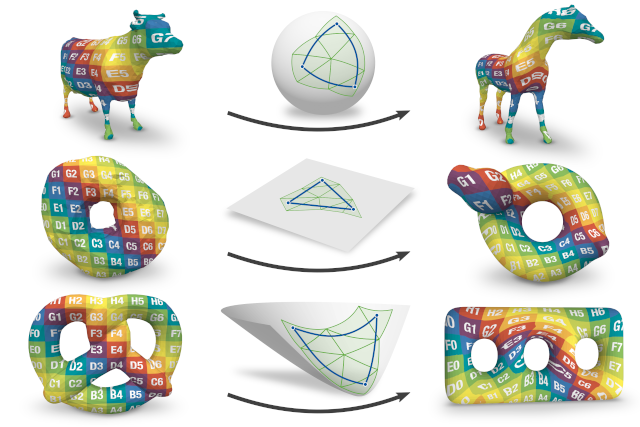
We propose a novel approach to represent maps between two discrete surfaces of the same genus and to minimize intrinsic mapping distortion. Our maps are well-defined at every surface point and are guaranteed to be continuous bijections (surface homeomorphisms). As a key feature of our approach, only the images of vertices need to be represented explicitly, since the images of all other points (on edges or in faces) are properly defined implicitly. This definition is via unique geodesics in metrics of constant Gaussian curvature. Our method is built upon the fact that such metrics exist on surfaces of arbitrary topology, without the need for any cuts or cones (as asserted by the uniformization theorem). Depending on the surfaces' genus, these metrics exhibit one of the three classical geometries: Euclidean, spherical or hyperbolic. Our formulation handles constructions in all three geometries in a unified way. In addition, by considering not only the vertex images but also the discrete metric as degrees of freedom, our formulation enables us to simultaneously optimize the images of these vertices and images of all other points.

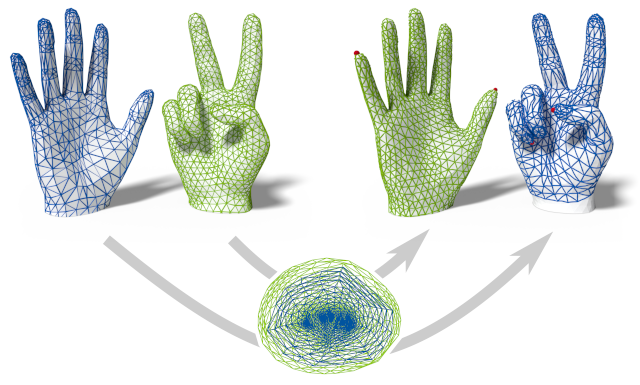
The problem of discrete surface parametrization, i.e. mapping a mesh to a planar domain, has been investigated extensively. We address the more general problem of mapping between surfaces. In particular, we provide a formulation that yields a map between two disk-topology meshes, which is continuous and injective by construction and which locally minimizes intrinsic distortion. A common approach is to express such a map as the composition of two maps via a simple intermediate domain such as the plane, and to independently optimize the individual maps. However, even if both individual maps are of minimal distortion, there is potentially high distortion in the composed map. In contrast to many previous works, we minimize distortion in an end-to-end manner, directly optimizing the quality of the composed map. This setting poses additional challenges due to the discrete nature of both the source and the target domain. We propose a formulation that, despite the combinatorial aspects of the problem, allows for a purely continuous optimization. Further, our approach addresses the non-smooth nature of discrete distortion measures in this context which hinders straightforward application of off-the-shelf optimization techniques. We demonstrate that, despite the challenges inherent to the more involved setting, discrete surface-to-surface maps can be optimized effectively.

Pa­ra­met­ri­za­tion based methods have recently become very popular for the generation of high quality quad meshes. In contrast to previous approaches, they allow for intuitive user control in order to accommodate all kinds of application driven constraints and design intentions. A major obstacle in practice, however, are the relatively long computations that lead to response times of several minutes already for input models of moderate complexity. In this paper we introduce a novel strategy to handle highly complex input meshes with up to several millions of triangles such that quad meshes can still be created and edited within an interactive workflow. Our method is based on representing the input model on different levels of resolution with a mechanism to propagate pa­ra­met­ri­za­tions from coarser to finer levels. The major challenge is to guarantee consistent pa­ra­met­ri­za­tions even in the presence of charts, transition functions, and singularities. Moreover, the remaining degrees of freedom on coarser levels of resolution have to be chosen carefully in order to still achieve low distortion pa­ra­met­ri­za­tions. We demonstrate a prototypic system where the user can interactively edit quad meshes with powerful high-level operations such as guiding constraints, singularity repositioning, and singularity connections.