Publications

A new stationary subdivision scheme is presented which performs slower topological refinement than the usual dyadic split operation. The number of triangles increases in every step by a factor of 3 instead of 4. Applying the subdivision operator twice causes a uniform refinement with tri-section of every original edge (hence the name sqrt(3)-subdivision) while two dyadic splits would quad-sect every original edge. Besides the finer gradation of the hierarchy levels, the new scheme has several important properties: The stencils for the subdivision rules have minimum size and maximum symmetry. The smoothness of the limit surface is C2 everywhere except for the extraordinary points where it is C1. The convergence analysis of the scheme is presented based on a new general technique which also applies to the analysis of other subdivision schemes. The new splitting operation enables locally adaptive refinement under built-in preservation of the mesh consistency without temporary crack-fixing between neighboring faces from different refinement levels. The size of the surrounding mesh area which is affected by selective refinement is smaller than for the dyadic split operation. We further present a simple extension of the new subdivision scheme which makes it applicable to meshes with boundary and allows us to generate sharp feature lines.

We present a novel algorithm to evaluate and render Loop subdivision surfaces. The algorithm exploits the fact that Loop subdivision surfaces are piecewise polynomial and uses the forward difference technique for efficiently computing uniform samples on the limit surface. The main advantage of our algorithm is that it only requires a small and constant amount of memory that does not depend on the subdivision depth. The simple structure of the algorithm enables a scalable degree of hardware implementation. By low-level parallelization of the computations, we can reduce the critical computation costs to a theoretical minimum of about one float[3]-operation per triangle.

While traditional computer aided design (CAD) is mainly based on piecewise polynomial surface representations, the recent advances in the efficient handling of polygonal meshes have made available a set of powerful techniques which enable sophisticated modeling operations on freeform shapes. In this tutorial we are going to give a detailed introduction into the various techniques that have been proposed over the last years. Those techniques address important issues such as surface generation from discrete samples (e.g. laser scans) or from control meshes (ab initio design); complexity control by adjusting the level of detail of a given 3D-model to the current application or to the available hardware resources; advanced mesh optimization techniques that are based on the numerical simulation of physical material (e.g. membranes or thin plates) and finally the generation and modification of hierarchical representations which enable sophisticated multiresolution modeling functionality. We present an interactive system for the generation of high quality triangle meshes that allows us to handle hybrid geometry (point clouds, polygons,...) as input data. In order to be able to robustly process huge data sets, we exploit graphics hardware features like the raster manager and the z-buffer for specific sub-tasks in the overall procedure. By this we significantly accelerate the stitching of mesh patches and obtain an algorithm for sub-sampling the data points in linear time. The target resolution and the triangle alignment in sub-regions of the resulting mesh can be controlled by adjusting the screen resolution and viewing transformation. An intuitive user interface provides a flexible tool for application dependent optimization of the mesh.

We present an interactive system for the generation of high quality triangle meshes that allows us to handle hybrid geometry (point clouds, polygons,...) as input data. In order to be able to robustly process huge data sets, we exploit graphics hardware features like the raster manager and the z-buffer for specific sub-tasks in the overall procedure. By this we significantly accelerate the stitching of mesh patches and obtain an algorithm for sub-sampling the data points in linear time. The target resolution and the triangle alignment in sub-regions of the resulting mesh can be controlled by adjusting the screen resolution and viewing transformation. An intuitive user interface provides a flexible tool for application dependent optimization of the mesh.

Multiresolution shape representation is a very effective way to decompose surface geometry into several levels of detail. Geometric modeling with such representations enables flexible modifications of the global shape while preserving the detail information. Many schemes for modeling with multiresolution decompositions based on splines, polygonal meshes and subdivision surfaces have been proposed recently. In this paper we modify the classical concept of multiresolution representation by no longer requiring a global hierarchical structure that links the different levels of detail. Instead we represent the detail information implicitly by the geometric difference between independent meshes. The detail function is evaluated by shooting rays in normal direction from one surface to the other without assuming a consistent tessellation. In the context of multiresolution shape deformation, we propose a dynamic mesh representation which adapts the connectivity during the modification in order to maintain a prescribed mesh quality. Combining the two techniques leads to an efficient mechanism which enables extreme deformations of the global shape while preventing the mesh from degenerating. During the deformation, the detail is reconstructed in a natural and robust way. The key to the intuitive detail preservation is a transformation map which associates points on the original and the modified geometry with minimum distortion. We show several examples which demonstrate the effectiveness and robustness of our approach including the editing of multiresolution models and models with texture.

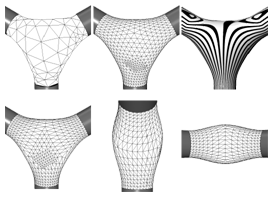
In this paper we present a new algorithm for smoothing arbitrary triangle meshes while satisfying G^1 boundary conditions. The algorithm is based on solving a non-linear fourth order partial differential equation (PDE) that onlydepends on intrinsic surface properties instead of being derived from a particular surface parameterization. This continuous PDE has a (representation-independent) well-defined solution which we approximate by our triangle mesh. Hence, changing the mesh complexity (refinement) or the mesh connectivity (remeshing) lead to just another discretization of the same smooth surface and doesn't affect the resulting geometric shape beyond this. This is typically not true for filter-based mesh smoothing algorithms. To simplify the computation we factorize the fourth order PDE into a set of two nested second order problems thus avoiding the estimation of higher order derivatives. Further acceleration is achieved by applying multigrid techniques on a fine-to-coarse hierarchical mesh representation.

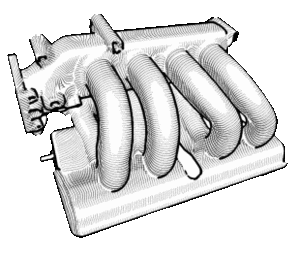
We present an interactive system for computer aided generation of line art drawings to illustrate 3D models that are given as triangulated surfaces. In a preprocessing step an enhanced 2D view of the scene is computed by sampling for every pixel the shading, the normal vectors and the principal directions obtained from discrete curvature analysis. Then streamlines are traced in the 2D direction fields and are used to define line strokes. In order to reduce noise artifacts the user may interactively select sparse reference lines and the system will automatically fill in additional strokes. By exploiting the special structure of the streamlines an intuitive and simple tone mapping algorithm can be derived to generate the final rendering.

We present a technique for remeshing irregular triangles meshes where the distribution and alignment can be adapted to the underlying geometry. Following the interactive virtual range scanner approach we overcome aliasing problems by introducing a special sampling technique. A sampling grid that can be aligned to the local features of the mesh is constructed interactively in an intuitive way and without adding reasonable overhead to the virtual scanning process.

In this paper we present a new algorithm to create fair discrete surfaces satisfying prescribed G1 boundary constraints. All surfaces are built by discretizing a partial differential equation based on pure geometric intrinsics. The construction scheme is designed to produce meshes that are partitioned into regular domains. Using this knowledge in advance we can develop a fast iterative algorithm resulting in surfaces of high aesthetic quality that have no local mean curvature extrema in the interior.

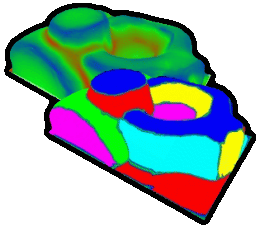
Triangle meshes are a popular representation of surfaces in computer graphics. Our aim is to detect feature on such surfaces. Feature regions distinguish themselves by high curvature. We are using discrete curvature analysis on triangle meshes to obtain curvature values in every vertex of a mesh. These values are then thresholded resulting in a so called binary feature vector. By adapting morphological operators to triangle meshes, noise and artifacts can be removed from the feature. We introduce an operator that determines the skeleton of the feature region. This skeleton can then be converted into a graph representing the desired feature. Therefore a description of the surface's geometrical characteristics is constructed.

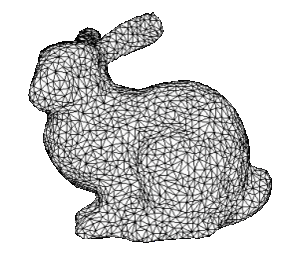
The representation of free-form surfaces by sufficiently refined polygonal meshes has become common in many geometric modeling applications where complicated objects have to be handled. While working with triangle meshes is flexible and efficient, there are difficulties arising prominently from the lack of infinitesimal smoothness and the prohibitive complexity of highly detailed 3D-models. In this paper we discuss the generation of fair triangle meshes which are optimal with respect to some discretized curvature energy functional. The key issues are the proper definition of discrete curvature, the smoothing of high resolution meshes by solving a sparse linear system that characterizes the global minimum of an energy functional. Results and techniques from differential geometry, variational surface design (fairing), and numerical analysis are combined to find efficient and robust algorithms that generate smooth meshes of arbitrary topology which interpolate or approximate a given set of data points.

In this paper we present a hierarchical approach for the deformable surface technique. This technique is a three dimensional extension of the snake segmentation method. We use it in the context of visualizing three dimensional scalar data sets. In contrast to classical indirect volume visualization methos, this reconstruction is not based on iso-values but on boundary information derived from discontinuities in the data. We propose a mulitlevel adaptive finite difference solver, which generates a target surface minimizing an energy functional based on an internal energy of the surface and an outer energy induced by the gradient of the volume. The method is attractive for preprocessing in numerical simulation or texture mapping. Red-green triangulation allows adaptive refinement of the mesh. Special considerations help to prevent self interpenetration of the surfaces. We will also show some techniques that introduce the hierarchical aspect into the inhomogeneity of the partial differential equation. The approach proves to be appropriate for data sets that contain a collection of objects separated by distinct boundaries. Thes kind of data sets often occur in medical and technical tomography, as we will demonstrate in a few examples.