Distortion-Minimizing Injective Maps Between Surfaces

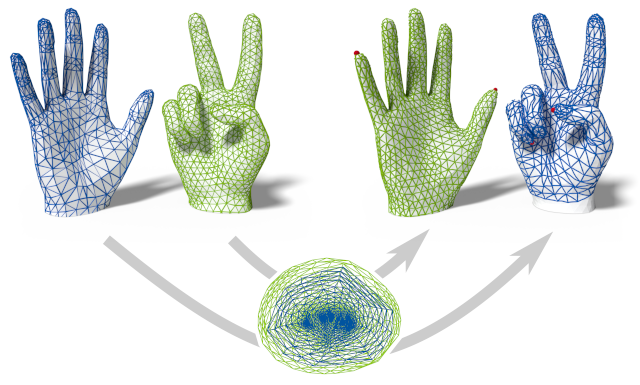
The problem of discrete surface parametrization, i.e. mapping a mesh to a planar domain, has been investigated extensively. We address the more general problem of mapping between surfaces. In particular, we provide a formulation that yields a map between two disk-topology meshes, which is continuous and injective by construction and which locally minimizes intrinsic distortion. A common approach is to express such a map as the composition of two maps via a simple intermediate domain such as the plane, and to independently optimize the individual maps. However, even if both individual maps are of minimal distortion, there is potentially high distortion in the composed map. In contrast to many previous works, we minimize distortion in an end-to-end manner, directly optimizing the quality of the composed map. This setting poses additional challenges due to the discrete nature of both the source and the target domain. We propose a formulation that, despite the combinatorial aspects of the problem, allows for a purely continuous optimization. Further, our approach addresses the non-smooth nature of discrete distortion measures in this context which hinders straightforward application of off-the-shelf optimization techniques. We demonstrate that, despite the challenges inherent to the more involved setting, discrete surface-to-surface maps can be optimized effectively.