Publications

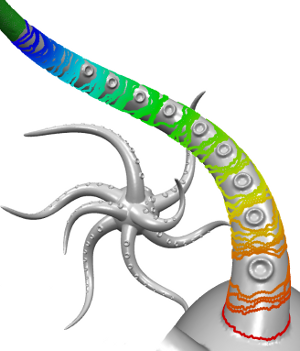
We present a novel approach to feature-aware mesh deformation. Previous mesh editing methods are based on an elastic deformation model and thus tend to uniformly distribute the distortion in a least squares sense over the entire deformation region. Recent results from image resizing, however, show that discrete local modifications like deleting or adding connected seams of image pixels in regions with low saliency lead to far superior preservation of local features compared to uniform scaling -- the image retargeting analogon to least squares mesh deformation. Hence, we propose a discrete mesh editing scheme that combines elastic as well as plastic deformation (in regions with little geometric detail) by transferring the concept of seam carving from image retargeting to the mesh deformation scenario. A geometry seam consists of a connected strip of triangles within the mesh's deformation region. By collapsing or splitting the interior edges of this strip we perform a deletion or insertion operation that is equivalent to image seam carving and can be interpreted as a local plastic deformation. We use a feature measure to rate the geometric saliency of each triangle in the mesh and a well-adjusted distortion measure to determine where the current mesh distortion asks for plastic deformations, i.e., for deletion or insertion of geometry seams. Precomputing a fixed set of low-saliency seams in the deformation region allows us to perform fast seam deletion and insertion operations in a predetermined order such that the local mesh modifications are properly restored when a mesh editing operation is (partially) undone. Geometry seam carving hence enables the deformation of a given mesh in a way that causes stronger distortion in homogeneous mesh regions while salient features are preserved much better.

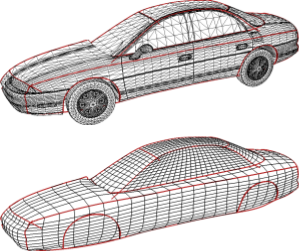
In this paper, we present a semi-automatic approach to efficiently and robustly recover the characteristic feature curves of a given free-form surface where we do not have to assume that the input is a proper manifold. The technique supports a sketch-based interface where the user just has to roughly sketch the location of a feature by drawing a stroke directly on the input mesh. The system then snaps this initial curve to the correct position based on a graph-cut optimization scheme that takes various surface properties into account. Additional position constraints can be placed and modified manually which allows for an interactive feature curve editing functionality. We demonstrate the usefulness of our technique by applying it to two practical scenarios. At first, feature curves can be used as handles for surface deformation, since they describe the main characteristics of an object. Our system allows the user to manipulate a curve while the underlying non-manifold surface adopts itself to the deformed feature. Secondly, we apply our technique to a practical problem scenario in reverse engineering. Here, we consider the problem of generating a statistical (PCA) shape model for car bodies. The crucial step is to establish proper feature correspondences between a large number of input models. Due to the significant shape variation, fully automatic techniques are doomed to failure. With our simple and effective feature curve recovery tool, we can quickly sketch a set of characteristic features on each input model which establishes the correspondence to a pre-defined template mesh and thus allows us to generate the shape model. Finally, we can use the feature curves and the shape model to implement an intuitive modeling metaphor to explore the shape space spanned by the input models.

The paper is an extended version of the paper "A sketching interface for feature curve recovery of free-form surfaces" published at the 2009 SIAM/ACM Joint Conference on Geometric and Physical Modeling. In this extended version, we presend a second application where we use the recovered feature curves as modeling handles for surface deformation.