Approximation and Visualization of Discrete Curvature on Triangulated Surfaces
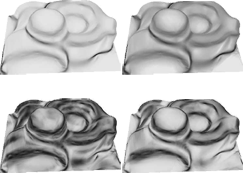
Triangle meshes are a facile and effective representation for many kinds of surfaces. In order to rate the quality of a surface, the calculation of geometric curvatures as there are defined for smooth surfaces is useful an necessary for a variety of applications. We investigate an approach to locally approximate the first and second fundamental forms at every (inner) vertex of a triangle mesh. We use locally isometric divided difference operators, where we compare two variants of parameterizations (tangent plane and exponential map) by testing on elementary analytic surfaces. We further describe a technique for visualizing the resulting curvature data. A simple median filter is used to effectively filter noise from the input data. According to application dependent requirements a global or a pervertex local color coding can be provided. The user may interactively modify the color transfer function, enabling him or her to visually evaluate the quality of triangulated surfaces.

