Geometric Fairing of Irregular Meshes for Free-Form Surface Design

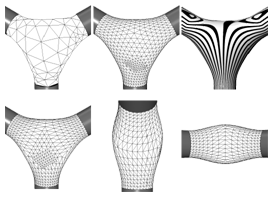
In this paper we present a new algorithm for smoothing arbitrary triangle meshes while satisfying G^1 boundary conditions. The algorithm is based on solving a non-linear fourth order partial differential equation (PDE) that onlydepends on intrinsic surface properties instead of being derived from a particular surface parameterization. This continuous PDE has a (representation-independent) well-defined solution which we approximate by our triangle mesh. Hence, changing the mesh complexity (refinement) or the mesh connectivity (remeshing) lead to just another discretization of the same smooth surface and doesn't affect the resulting geometric shape beyond this. This is typically not true for filter-based mesh smoothing algorithms. To simplify the computation we factorize the fourth order PDE into a set of two nested second order problems thus avoiding the estimation of higher order derivatives. Further acceleration is achieved by applying multigrid techniques on a fine-to-coarse hierarchical mesh representation.