Publications

Direction fields and vector fields play an increasingly important role in computer graphics and geometry processing. The synthesis of directional fields on surfaces, or other spatial domains, is a fundamental step in numerous applications, such as mesh generation, deformation, texture mapping, and many more. The wide range of applications resulted in definitions for many types of directional fields: from vector and tensor fields, over line and cross fields, to frame and vector-set fields. Depending on the application at hand, researchers have used various notions of objectives and constraints to synthesize such fields. These notions are defined in terms of fairness, feature alignment, symmetry, or field topology, to mention just a few. To facilitate these objectives, various representations, discretizations, and optimization strategies have been developed. These choices come with varying strengths and weaknesses. This course provides a systematic overview of directional field synthesis for graphics applications, the challenges it poses, and the methods developed in recent years to address these challenges.

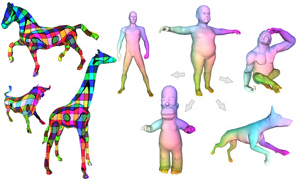
We introduce an efficient computational method for generating dense and low distortion maps between two arbitrary surfaces of same genus. Instead of relying on semantic correspondences or surface parameterization, we directly optimize a variance-minimizing transport plan between two input surfaces that defines an as-conformal-as-possible inter-surface map satisfying a user-prescribed bound on area distortion. The transport plan is computed via two alternating convex optimizations, and is shown to minimize a generalized Dirichlet energy of both the map and its inverse. Computational efficiency is achieved through a coarse-to-fine approach in diffusion geometry, with Sinkhorn iterations modified to enforce bounded area distortion. The resulting inter-surface mapping algorithm applies to arbitrary shapes robustly, with little to no user interaction.

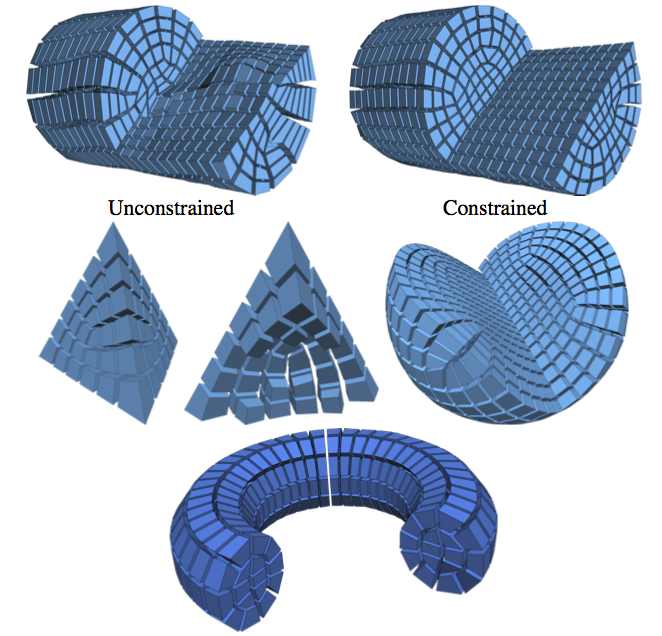
The computation of smooth fields of orthogonal directions within a volume is a critical step in hexahedral mesh generation, used to guide placement of edges and singularities. While this problem shares high-level structure with surface-based frame field problems, critical aspects are lost when extending to volumes, while new structure from the flat Euclidean metric emerges. Taking these considerations into account, this paper presents an algorithm for computing such “octahedral” fields. Unlike existing approaches, our formulation achieves infinite resolution in the interior of the volume via the boundary element method (BEM), continuously assigning frames to points in the interior from only a triangle mesh discretization of the boundary. The end result is an orthogonal direction field that can be sampled anywhere inside the mesh, with smooth variation and singular structure in the interior even with a coarse boundary. We illustrate our computed frames on a number of challenging test geometries. Since the octahedral frame field problem is relatively new, we also contribute a thorough discussion of theoretical and practical challenges unique to this problem.