Singularity-Constrained Octahedral Fields for Hexahedral Meshing

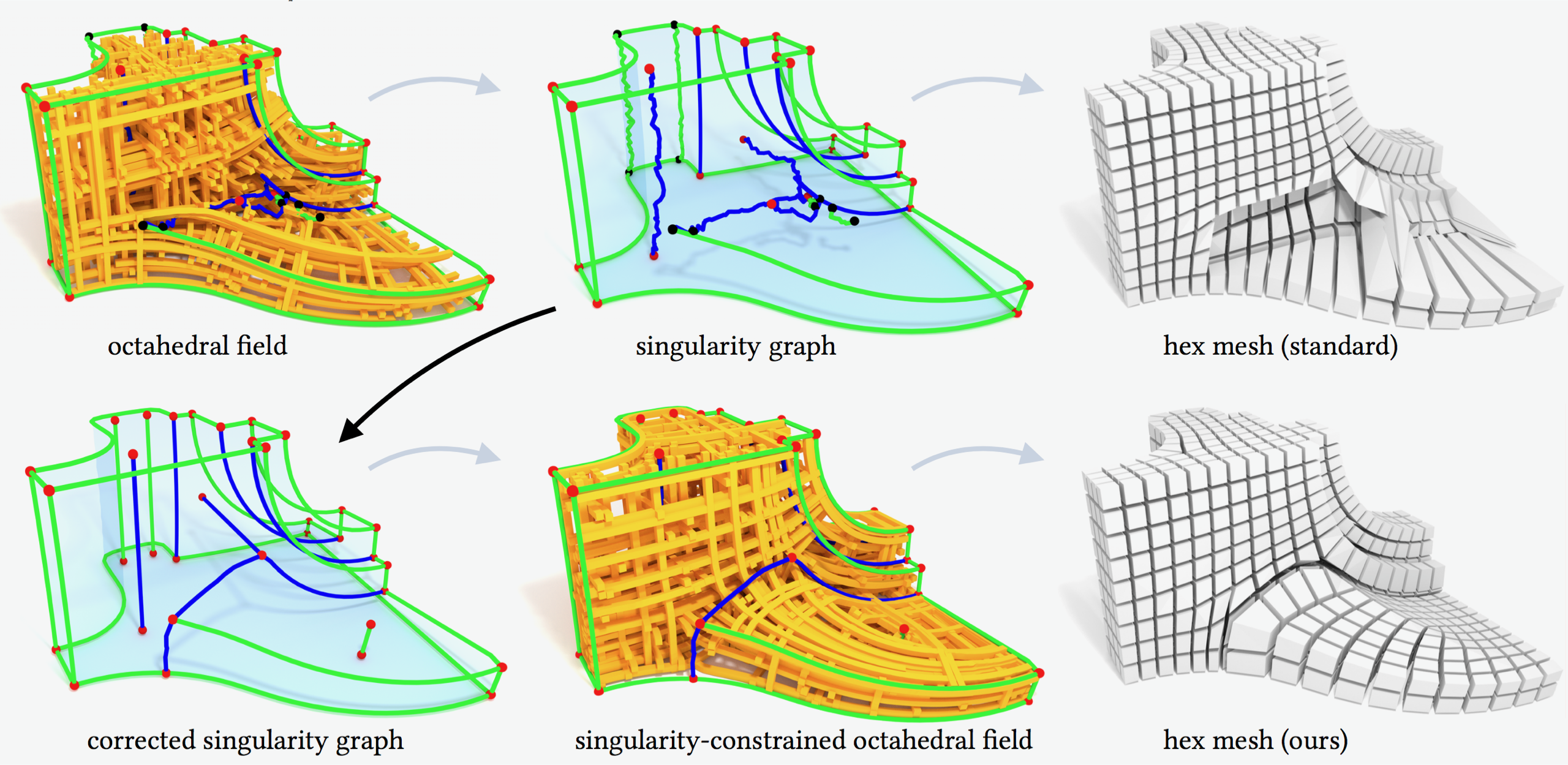
Despite high practical demand, algorithmic hexahedral meshing with guarantees on robustness and quality remains unsolved. A promising direction follows the idea of integer-grid maps, which pull back the Cartesian hexahedral grid formed by integer isoplanes from a parametric domain to a surface-conforming hexahedral mesh of the input object. Since directly optimizing for a high-quality integer-grid map is mathematically challenging, the construction is usually split into two steps: (1) generation of a surface-aligned octahedral field and (2) generation of an integer-grid map that best aligns to the octahedral field. The main robustness issue stems from the fact that smooth octahedral fields frequently exhibit singularity graphs that are not appropriate for hexahedral meshing and induce heavily degenerate integer-grid maps. The first contribution of this work is an enumeration of all local configurations that exist in hex meshes with bounded edge valence, and a generalization of the Hopf-Poincaré formula to octahedral fields, leading to necessary local and global conditions for the hex-meshability of an octahedral field in terms of its singularity graph. The second contribution is a novel algorithm to generate octahedral fields with prescribed hex-meshable singularity graphs, which requires the solution of a large non-linear mixed-integer algebraic system. This algorithm is an important step toward robust automatic hexahedral meshing since it enables the generation of a hex-meshable octahedral field.