Boundary Element Octahedral Fields in Volumes

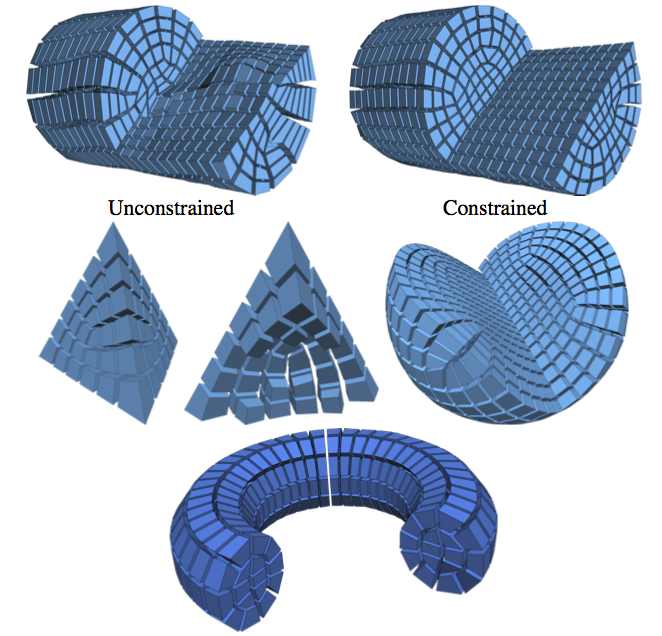
The computation of smooth fields of orthogonal directions within a volume is a critical step in hexahedral mesh generation, used to guide placement of edges and singularities. While this problem shares high-level structure with surface-based frame field problems, critical aspects are lost when extending to volumes, while new structure from the flat Euclidean metric emerges. Taking these considerations into account, this paper presents an algorithm for computing such “octahedral” fields. Unlike existing approaches, our formulation achieves infinite resolution in the interior of the volume via the boundary element method (BEM), continuously assigning frames to points in the interior from only a triangle mesh discretization of the boundary. The end result is an orthogonal direction field that can be sampled anywhere inside the mesh, with smooth variation and singular structure in the interior even with a coarse boundary. We illustrate our computed frames on a number of challenging test geometries. Since the octahedral frame field problem is relatively new, we also contribute a thorough discussion of theoretical and practical challenges unique to this problem.