Non-Linear Shape Optimization Using Local Subspace Projections

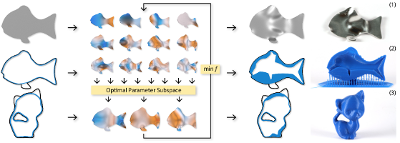
In this paper we present a novel method for non-linear shape opti- mization of 3d objects given by their surface representation. Our method takes advantage of the fact that various shape properties of interest give rise to underdetermined design spaces implying the existence of many good solutions. Our algorithm exploits this by performing iterative projections of the problem to local subspaces where it can be solved much more efficiently using standard numer- ical routines. We demonstrate how this approach can be utilized for various shape optimization tasks using different shape parameteri- zations. In particular, we show how to efficiently optimize natural frequencies, mass properties, as well as the structural yield strength of a solid body. Our method is flexible, easy to implement, and very fast.